



自由研究は理科のイメージが強いですが、他の教科に関するテーマもたくさんあります。
今回は、一般財団法人理数教育研究所が行っている、「算数・数学の自由研究」作品コンクール(MATHコン)を紹介します。
これまでの入賞作品からヒントを得て、身近な「なぜ?」「本当?」「どうなる?」を算数・数学の力を使って解き明かしてみましょう!
理数教育研究所は、子どもの科学する心を育み、数理的な知性を伸ばし、日本の教育に貢献することを目的として、2012年に設立されました。日本の理数教育の充実のため、研究・調査や研修・助成、広報誌の発刊などを行っています。
2013年から始まった「算数・数学の自由研究」作品コンクール(MATHコン)は、日常生活や学校で学んでいる時に感じた疑問や課題を、算数・数学の力を活用して探究し、気づいたことやわかったことをまとめたレポートを応募するコンクールです。最優秀作品には、旧文部省で小学校算術教科書を編集した塩野直道先生の名を冠した賞を授与し、優秀な作品は12月の表彰式で表彰します。
身の回りで不思議に思ったことや疑問を感じたことを見つけ、どうしたら解決できるかを考えます。そのために、数や計算、図形、データの活用などどんな手法が使えるかを検討しましょう。例えば、調べたいことが数で表せる時は数・計算を使いましょう。また、形に関する疑問なら図形の性質が使えます。そして、全体の傾向を調べたいならデータを活用すると良いでしょう。YouTubeの「MATHコン チャンネル」では、「テーマの見つけ方」や「レポートのまとめ方」などについて詳しく解説しているので、ぜひ参考にしてください。
研究のきっかけ
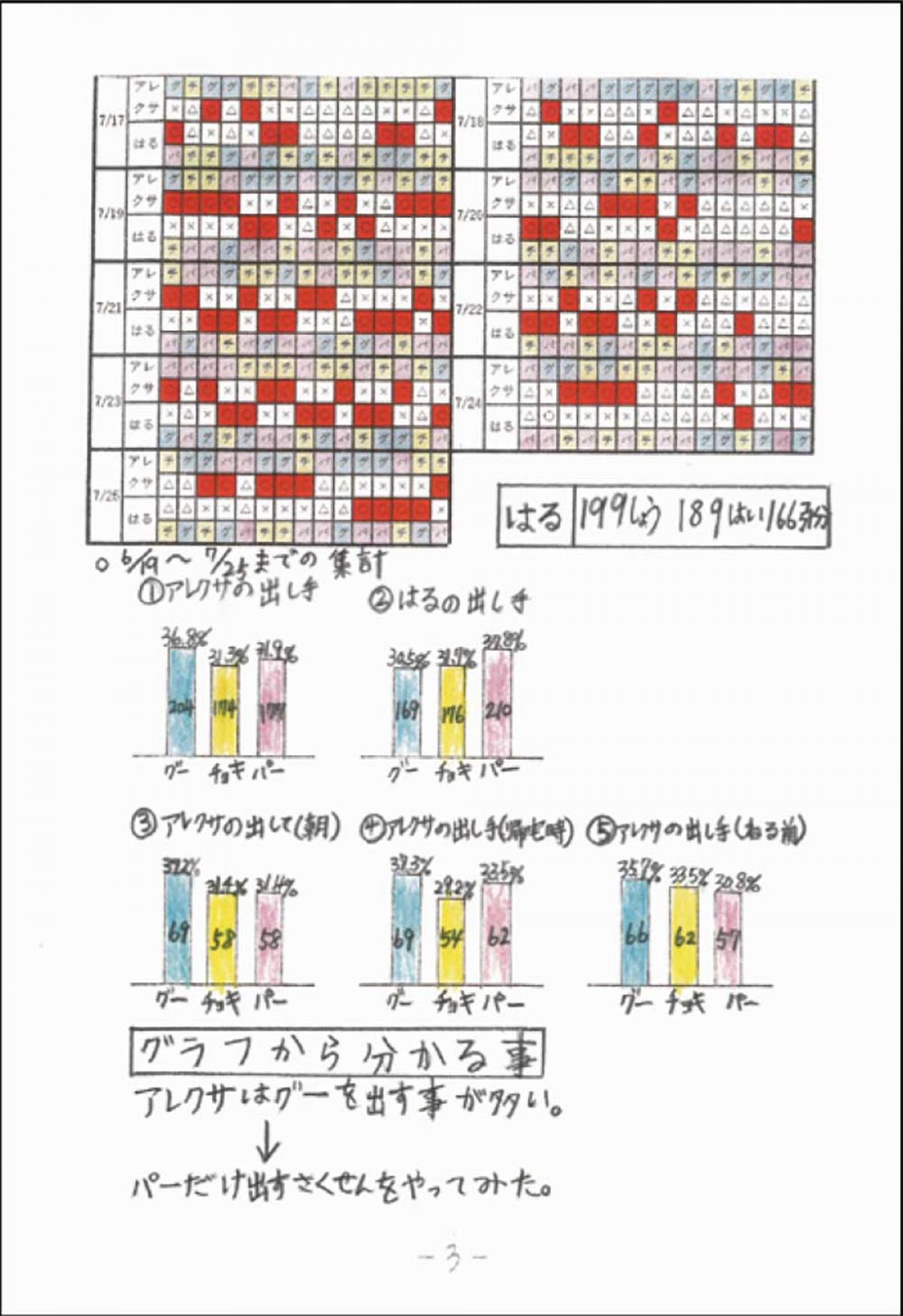
AIのかしこさにびっくりして、アレクサとじゃんけん対決をしてどれくらい勝てるのかなどを調べてみたいと思った。
研究の方法
①1日3回、5回ずつじゃんけんをする。
②アレクサが出した手を記録する。
③出した手を調べて、どうやったら勝てるか、特徴を見つける。
研究の内容
アレクサがグーを出すことが多かったので、後半からパーだけ出す作戦にしたら、今度はパーを出すことが多くなった。アレクサはこちらの手を分析しながら次の手を出し、勝ち負けが平等になるようにしている。
研究のまとめ・今後の課題
アレクサの1日ごとの勝ち負けの数はバラバラだけれど、合計すると勝ち負けを同じにしていることがわかった。もっと詳しく調べて勝てる作戦を考えたい。
講評
AIのアレクサとじゃんけん対決をして、アレクサの特徴を探った楽しい作品です。
約2か月を費やした熱意がすばらしい発見につながり、優れた自由研究になりました。
動機・目的
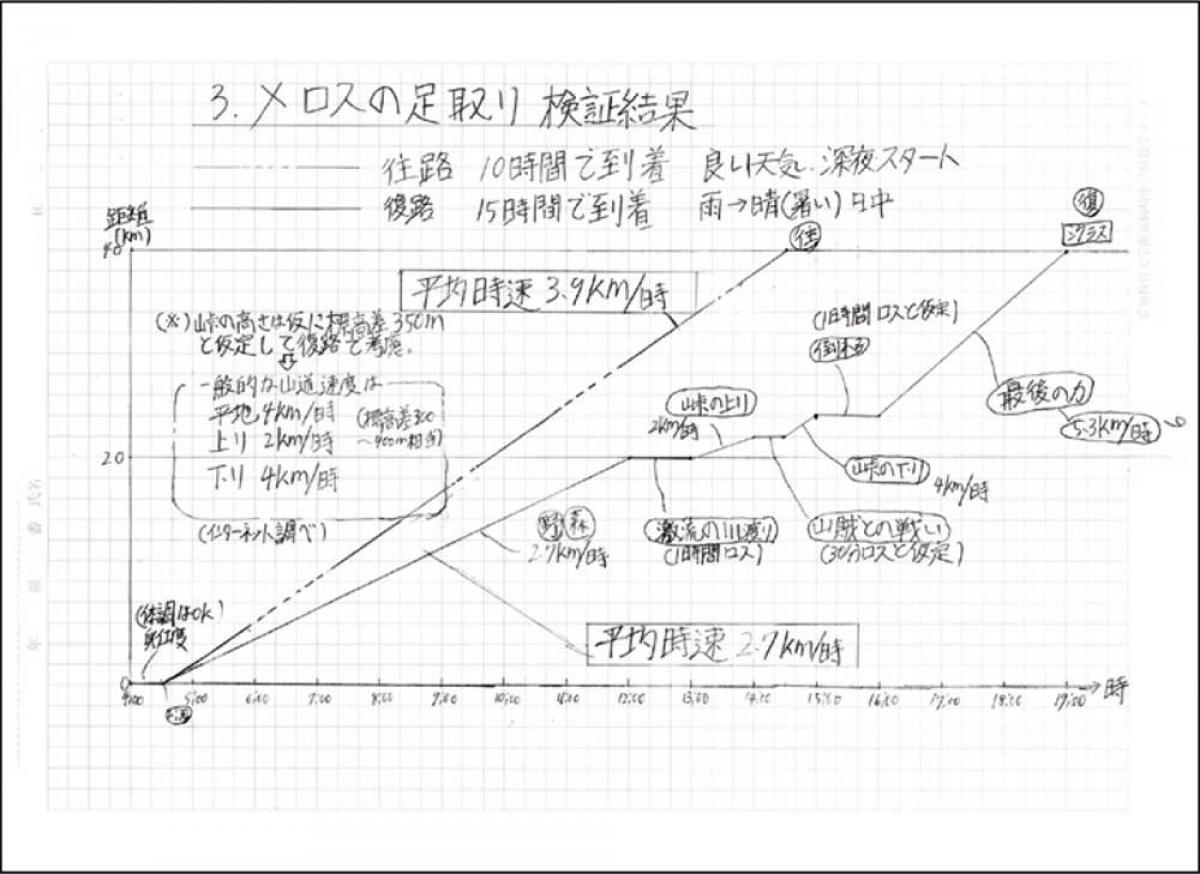
太宰治著『走れメロス』のメロスがどれほどの勢いで進んだのかを算出し、数値で彼の頑張りを感じたいと思い、メロスの足どりを検証した。
検証内容・結果
「初夏」「深夜出発」「十里の道」などの記述から、所要時間を推定、平均時速を算出し、結果をグラフにまとめた。平均時速は往路3.9㎞/時、復路2.7㎞/時となった。
考察・感想
一般男性の歩行速度やフルマラソンのタイムなどと比較し、メロスは全く全力で走っていないことがわかった。タイトルは「走れよメロス」の方があっているなと思った。
講評
作品の中に出てくる語句や文章から、場所、時刻、および距離を算出し、得られたデータから全行程をグラフに表してまとめています。文学作品をグラフまで利用して分析していて、主人公は全力で走っていたかどうかが客観的にわかります。
研究のきっかけ
バスケットボールやサッカーなどのスポーツで使うボールは、パネルの形や大きさ、組み合わせが違うのにどれも球になっている。どんな仕組みでできているのか不思議に思い、いろいろな球の仕組みを調べたり、自分で作ったりしたいと思った。
研究の方法
①いろいろなパネルの仕組みを調べる。
②「仕組みを調べて気づいたこと」「球技の種類によって異なる秘密」を調べる。
③いろいろな球を作ってみる。
研究の結果
パネルの形は1種類か2種類でできている、パネルの数は偶数枚になっていることなどに気づいた。パネルのデザインや枚数を考えてオリジナル球を作った。
研究のまとめ・感想
それぞれの球の使い方に合わせて、パネルの大きさや形、枚数、組み合わせを考えている。今回は実際にボールを切り開いたが、計算すれば材料を無駄にしないでボールを作れそう。約1か月の研究で、身近な生活の中にはいろいろな算数があって、役に立つかもしれないとわかった。
講評
実際に6つのボールを調べて「球の仕組みの秘密」に挑み、「球を作ろう」とした意欲的な研究です。
算数を活用して身近な生活への探究をしている点が評価されました。

研究の動機や目的
流れ星には「光っている間に願いごとを3回唱えれば叶う」という言い伝えがある。実際に3回も唱える余裕があるのか、できそうもないことの比喩として言われているだけではないかという疑問があり、確認することにした。
研究の方法や内容
①流れ星の発光時間を求める。
②人間の反応速度を求める。
③願いごとを3回唱える時間を求める。
研究の結果と考察
視野角120°の環境下において、流星体の大きさが充分で、最も長いコースをたどった場合、願いごと「成績が上がりますように」を、発光時間内に3回唱えることは可能とわかった。
感想と今後の課題
検証前の段階では、どのような状況下でも不可能であると想像していたので驚いた。コンピューターによるプログラムは父に協力してもらい、まだ一人で作成するのは難しい状況だが、これから勉強していきたい。
講評
「流れ星で願いを叶える」という誰もが知っている夢のあるテーマを選ぶ一方で、そもそもその前提条件である「3回願いを唱える」が実現できるものか?の問いに数学モデルと現実のデータを組み合わせて具体的な解を導いています。実際に実験環境を制作した点も高く評価できます。

SEARCH
CATEGORY
よく読まれている記事
KEYWORD